Alpha_1 Model Repository

Grandpa's Desk Toy

by
Tim Mueller

My Grandfather used to make toys like these in his woodworking shop. It is a simple, but interesting linkage. I remember that the sliders would just barely miss each other as you spun it around making it interesting to play with. I wanted to do two things in creating a model of this toy: 1) create a model where the motion of all the parts is entirely controlled by a single parameter of the model, and 2) create a parametric model so the sliders where as long as possible to create the impression that they will collide like my Grandfather's did.

Images

Here are links to some 24 bit images.

Animations

Here is a short animation (180K) of the toy in motion. There are 60 frames for one complete revolution of the handle.

About this Model

Parameterized Motion

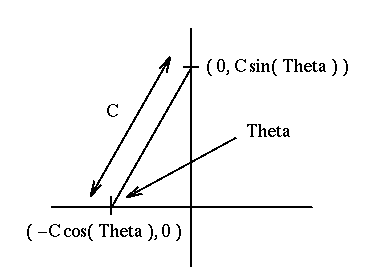The motion of this model is parameterized by one number which specifies the angle of the handle with respect to the axis of one of the slots. Other parameters, or dimensions, affect the sizes and shapes of the geometry of the model. In the figure on the right, the X and Y axes represent the axes of the slots. The dimension C is the distance between the center points of the sliders. The center points of the sliders (i.e., where the screws are) are easily calculated from the angle Theta as shown.

The positions of the sliders, the handle, the screws, and the knob are specified by these center points. By picking a fixed value for C and varying Theta from 0 to 360, the model is run through its full range of motion.

Here are some frames from the animation to illustrate:

Theta = 0 Theta = 60 Theta = 120 Theta = 180

Close But No Cigar (Collision)

The dimensions of the sliders are parametrically specified so that they just avoid collision. Using a pointed shape makes this more interesting. The first step is to determine the length H from the center of the slider to the tip as seen on the right. This is done for Theta = 45 to get the maximum.

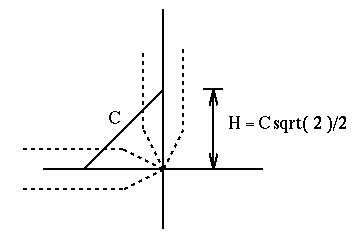
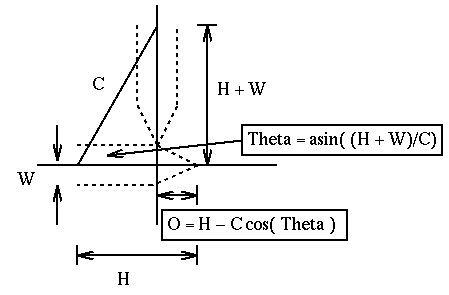
Next we look at the point where the tip of one slider would touch the side of the other slider. First we calculate the value for Theta at which this occurs. This is dependent on H, C, and W as seen on the left. Finally, we use this value of Theta to calculate O which is the offset distance used to create the point of the slider.

A shape for the sliders is now determined (by C and W) which will just avoid collision.
Now lets take a closer look at the animation and see if this works!

Variations

Now that we understand how the parameters (dimension) affect the model, we can make some variations on the design. From above, we see that Theta defines the motion and C and W define crucial parts of the geometry. The power of the parametric model is that once the relationships that characterize the design are defined (e.g., making the sliders as long as possible and just avoiding the collision), the specific values for the parameters can be altered to form new variants of the design.

In the original model seen in the images and animations above, the values of C and Ware:

C = 2.25
W = 0.25

We can define new variations of the model by altering just these two values. Here are two examples:

C = 2.25, W = 0.25(Original)	*C = 2.25, W = 0.5*	*C = 3.0, W = 0.5*

In addition to the obvious changes (the width of the slots, or the length of the handle), the "character" of the model is preserved (the "near collision" etc.) because this is explicitly represented in the parametric model. To show this, here is an animation of the version on the right of the above table.

Source File(s)

SCL file desk_toy.scl
Alpha_1 files (.a1)
- Original toy toy.a1
- Variation 1 (from table above) v1.a1
- Variation 2 (from table above) v2.a1
- Plain display table environment plain_display.a1
- Marble display table environment display.a1

Alpha_1 Model Repository Home Page

a1-web@gr.cs.utah.edu