The Alpha_1 system is an advanced research software base, supporting geometric modeling, high-quality graphics, curve and surface representations and algorithms, engineering design, analysis, visualization, process planning, and computer-integrated manufacturing.

Solid models in Alpha_1 are represented by trimmed B-spline (NURBS) sculptured surface boundary representations. NURBS are Non-Uniform knot vector, Rational B-Splines of arbitrary order with tensor-product surfaces trimmed by NURBS curves.

An extensive 2D and 3D geometric modeling environment supports user-oriented operations for building up parts from dimensions, through basic geometry (points, lines, arcs, circles, etc.) through curve and surface constructions (profiles, sweeps, extrusions, etc.), shape operations (bend, twist, warp, etc.), and finally solids and boolean expressions (union, intersection, and difference) of solids. Time-varying models support animation, linkage design, simulations, etc. Volume primitives (box, cylinder, sphere, etc.) are represented by "parametric object types" which generate and cache spline-surfaced solid representations on demand. Similarly, mechanical design "features" (holes, pockets, etc.) may be grouped to support automatic NC code generation within a context of machine setups, fixturing, etc.

The Alpha_1 distribution is a periodic release of the central, user-level applications of the general research system. This is a subset of the research system which is mainly aimed at mechanical engineering and computer science users.

Project Goals

The Alpha_1 project began in 1980 with a number of major goals. The first was producing a spline based, boundary representation solid modeler that could be used to model a large class of sculptured mechanical parts. Objects which fall into this category are abundant in the aerospace and automobile industries. Even parts that have, at first glance, a simple geometry sometimes cannot be accurately modeled without sculptured surfaces.

Alpha_1 also proposed to demonstrate the utility of high quality graphics in the mechanical design process, particularly when dealing with sculptured surfaces. Proper perception of a complex shape is not possible from a line drawing or rough shaded rendering. The perception of the shape of a sculptured object depends on an accurate model and an accurate rendering of the model.

Over the years, the project has included research in a variety of application areas. The most important of these is the manufacturing process which must be applied after a part is designed. Alpha_1 contains some advanced capabilities for generating manufacturing process plans and NC toolpaths directly from the geometric models created in the system.

Alpha_1 is also intended to serve as an experimental testbed on which new modeling ideas and techniques can be easily mounted and evaluated.

General Principles

This section describes a few general principles that will help you to understand how the system is structured and what some of the biases are.

B-Splines in Alpha_1

The initial surface representation upon which the Alpha_1 system was built, and the only surface type supported by the entire system, is the rational parametric tensor product B-spline surface.

B-splines have a number of desirable properties for use in computer-aided geometric design. First, splines provide inherent control of smoothness (degree of continuity).

Second, B-splines have the convex hull property: the curve always lies within a convex set determined by the parameters of the curve. It is therefore easy to bound the curve, simplifying many calculations.

Another feature of B-splines that is useful in a design system is "local control." Changing the location of a single control point modifies only a portion of the curve; the rest of the curve remains unchanged. This allows, for example, a designer to shape one region of a curve without affecting other regions that may be already complete.

The use of rational B-splines allows the exact representation of a large class of shapes, including the common quadric surfaces such as spheres, cylinders and cones. Since many common mechanical parts have circular cross sections, it is critical that a design system be able to reproduce such shapes.

A B-spline may be evaluated by computing the value at any given point. Often, however, an approximation to the entire curve or surface is desired. This may be found via a "subdivision" or "refinement" process. The Oslo Algorithm provides a method for taking a B-spline and computing a new B-spline, point for point identical to the original, but with more knots, and therefore more control points and more polynomial spans. It can be used to split, or subdivide, a B-spline into two pieces that, together, make up the original. The new control polygon, formed by joining the control points in order, more closely approximates the curve than did the original. Thus, by adding enough new knots, the control polygon itself may be used as an approximation to the curve.

Alpha_1 attempts to hide the details of the spline representation from users whenever possible, so a further discussion of splines is left for an appendix (Spline Introduction). Beginning users can probably get by for quite a while without reading the appendix, but advanced users will want to gain some familiarity with the material. The appendix is an informal and very basic introduction with the goal of providing just enough information so the system can be used effectively.

Parametric Modeling

Parametric modeling in the context of the Alpha_1 system means that the definition of a geometric part is considered more to be the parameters and relationships which generated it, rather than the low-level numeric data such as point coordinates, line equation coefficients, or spline data which are derived from those parameters. A surface of revolution, for example, may be represented as a set of sampled data points or as a set of spline surfaces. However, neither of these forms is likely to convey the information that the object has rotational symmetry. That information is retained in the parametric description of the object, and may be important for future evaluation, analysis, or documentation.

In addition to retaining a high-level description of an object, parametric modeling can be used to develop families of parts. This is sometimes called variational modeling. For example, the design of an object may involve definition of a number of dimensions and other parameters which affect the shape of the object. If one of these parameters or dimensions is changed, the set of commands which perform the construction can be re-executed to generate a related object with different dimensions. In this way, families of similar parts are naturally supported, as well as allowing parameters to be easily adjusted during the course of the design.

Dependency Propagation

Adjusting a dimension or parameter in the middle of a design is such a common operation that a mechanism is provided for automatically regenerating all the parts of a model which depend upon a parameter. During interactive modeling, the relationships between objects are recorded. If a basic dimension or parameter is changed later, the model is automatically updated to maintain the relationships. This is called dependency progagation.

Set Operations

The ability to perform set operations (union, intersection, and difference), on models is recognized as one of the important characteristics of a solid modeling system. Set operations perform a number of useful functions in the modeling process. They can be used to combine simpler objects into more complex ones. It is not necessary to design an entire object in one piece; it may be broken down into simpler components that can be designed independently. Thus, set operations provide a facility for modular design. Set operations may be used to model certain common machining operations. For example, set difference models material removal processes such as drilling or milling. Set union may be used to model gluing or welding type operations. Difference operations can be used for illustrative and analytical purposes as well, such as cross-section renderings and finite element analysis.

Performing set operations in a boundary modeling system requires computing the boundary of the result of the set operation. The boundary of the result must be composed of pieces of the boundaries of the operands, and these pieces must be bounded by intersection curves between the boundaries of the operands. Unfortunately, computing the exact intersection curve between two B-splines exactly is an intractable problem. The intersection can, however, be approximated to any desired precision.

The Alpha_1 system has the ability to perform set operations on "partially bounded sets." As long as they satisfy certain loose criteria, boundaries of objects to be combined by set operations need not be closed. This is a convenient feature for the designer, who is not forced to close object boundaries just so that set operations may be performed.

Graphics

A key concept put forth by the Alpha_1 project is that design of mechanical parts and, in particular, of sculptured mechanical parts, is greatly aided by high quality graphic rendering of the model. The shape of the model can be perceived more accurately and errors in the design found sooner if the designer can better visualize the model being created.

Where possible (on high-end workstations) interactive shaded rendering is supported as part of the interactive modeling environment. In addition, the Alpha_1 system incorporates a scanline rendering program that produces accurate shaded images of B-spline surfaces by adaptively subdividing surfaces into polyhedral approximations. The program has many options to control the polyhedral approximation, the rendering process, the lighting model, the surface characteristics, and the output form. It is possible to specify transparent or semi-transparent surfaces, allowing the designer to see interior details as well. Control over the lighting allows careful placement of highlights to give maximum shape information.

Alpha_1 also includes a ray tracing program for extremely high quality images. Images created with this program may include shadows, reflections, texture mapping, and other features not available in the scanline rendering program. These images naturally take much longer to generate.

Geometric Editor

The geometric editor for Alpha_1 is the c_shape_edit program. This program embodies many of the above principles and is the central application program in the Alpha_1 system. It is an interactive program with an interpreted command language which supports the principles of design with B-splines, parametric modeling, dependency propagation, set operations, and accurate rendering.

Many tools and operations are provided for shape definition. These include traditional 2D geometry, shape modification operations and 3D primitive objects.

The 2D geometry is supported by providing a number of drafting type operations that deal with points, lines, and arcs in the plane. Arcs and line segments may be chained together into a B-spline curve. Curves can be used to construct surfaces in many ways, including extrusions and general sweeps.

To simplify the task of working with B-spline surfaces, high level shape modification and design operators have been created such as bend, warp, and taper.

For those cases when basic 3D primitives are desired, operators are included for creating these. These include boxes, spheres and ellipsoids, cylinders and cones, and tori. The surfaces of the primitives are represented as B-splines, so any of the shape modification or set operators can be applied to them.

Finally, a large collection of mechanical features (various types of holes, pockets, grooves, etc.) is provided along with operations for creating manufacturing process plans from them.

All of these operations are provided in a unified way so that they interact to form a powerful set of design capabilities. Two-dimensional drafting style constructions can be extruded to form surfaces which can be bent or warped. The boolean set operations can be applied to surfaces produced from any of the other operations.

System Overview

The following figure illustrates the major components of the Alpha_1 system and their relationships.

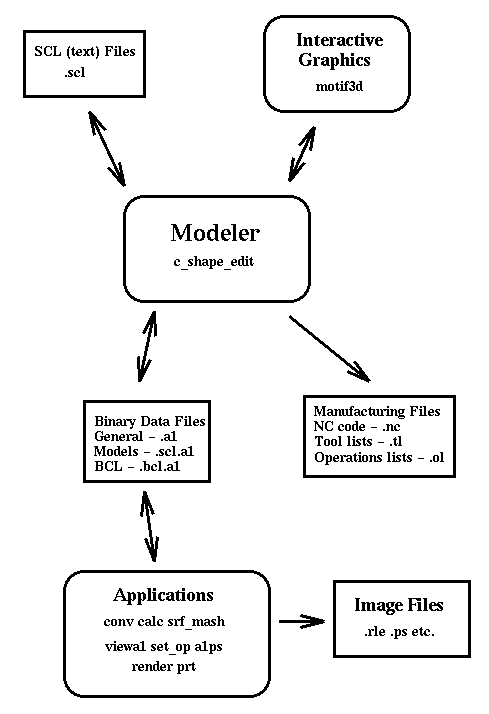
The central program is c_shape_edit, the interactive, interpreted environment which contains the commands for creating and modifying models. The interpreted command language is called SCL (c_Shape_edit Command Language). C_shape_edit has no direct graphics capabilities, so interactive graphical display is provided by a companion application called motif3d.

Motif3d establishes a communication channel with c_shape_edit and responds to a set of SCL commands to handle graphical display of the models in c_shape_edit. Motif3d provides a graphical interface (based on the X Window System and Motif) to interactive 3D view manipulation, animation previewing, basic I/O, etc. On high-end workstations, hardware accelerated graphics is supported for displaying the geometric models.

With this client-server approach it is possible for many "client" programs (such as motif3d) to communicate with c_shape_edit (the "server") at once. It is also possible to create graphical user interfaces to the SCL modeling environment using this approach, but no general purpose graphical interface is supported at this time.

When using the command language, the commands are usually entered with a standard emacs text editor. The resulting file contains all the commands which were used to generate the model. These can be saved in SCL files which use the ".scl" file name extension (as shown in the upper left portion of above figure). This is the high-level parametric model (see Parametric Modeling above) and sometimes called the unevaluated model because it expresses the relationships between objects, and not their values. For example, an SCL file might express the relationship that a line l passes through two points p and q as opposed to the evaluation of that relationship that determines what the line equation of l is. As the highest level description of a model, it is the most amenable to editing and modifications.

Once a model has been created in c_shape_edit, there is a large group of application and utility programs which can be used. Some of these are shown as examples in the figure above, but this is not a complete set. In order to access any of these programs, a binary evaluated model data file must be saved from c_shape_edit. These files are given a name with the ".a1" extension, and contain the resulting geometry which was computed by c_shape_edit. These data files can be given as input to programs which perform such functions as:

interactive viewing
shaded rendering
ray tracing
mass property calculations
set operations
tessellation (converting surfaces to polygons)
postscript printing
manufacturing post processing

The binary ".a1" files which are used by these programs generally do not contain the parametric definition of the model, but the evaluation of the model. These ".a1" files can easily be regenerated from the ".scl" file with c_shape_edit should editing be required. A particular form of the binary ".a1" is available from c_shape_edit which does store the parametric relationships of the model as well as the evaluations of those relationships. These are by convention labeled with the ".scl.a1" file name extension. When starting a new modeling session, these files can be reloaded into a c_shape_edit to restore the model and all it's relationships without re-executing a large ".scl" file.

The ".a1" file is the general binary form of data exchange between Alpha_1 applications. Alpha_1 binary files are machine independent and can be shared if the system is installed on multiple platforms. A text form of the ".a1" files does exist, because interfaces to non-Alpha_1 utilities are often simpler to manage with a text form. The conv program converts back and forth between the binary and text forms. The text form is considered temporary, and may change without notice. Long-term storage of ".a1" files should always be in the binary form.

The process planning and manufacturing capabilities of Alpha_1 may also be used to generate files for scheduling, setting up, and running NC machines. Some of the files generated for this purpose are ".nc" files. They are not read by the other Alpha_1 utility programs (except for some simulation).

The render and ray tracing programs produce ".rle" (for Run-Length Encoded) image files, which are in the Utah Raster Toolkit (URT) format. URT is a separate software system which is distributed with Alpha_1 as well as independently. A whole suite of URT programs are available for manipulating these image files.

Alpha_1 User's Manual Home Page

a1-web@gr.cs.utah.edu