Solid Modeling

One of the most commonly used operations for constructing complex parts (and especially mechanical parts) is the set operation or boolean operation. There are two ways to do this kind of operation in Alpha_1. The first is to use the c_shape_edit combineShells procedure which will be described here, just as any other modeling operation is used. The second method is to define all the component pieces in c_shape_edit modeler, dump them into a file and use the set_op program to compute the boolean results. In this section we describe using set operations from within c_shape_edit.

Table of contents for this page:

combineShells operation

combinerCrvs operation

Basic Boolean Operations

Multiple Operations

Cross Section Views

Common Problems

Adjacencies

Invoking combineShells in the c_shape_edit modeler.

The combineShells, combinerCrvs operation will perform the requested operation between two objects which are either shells, volume primitives, or mechanical features.

combineShells( Shl1, Shl2, Operation, TriApxFlag, Res )

Returns

<shell> Perform the requested operation on the two arguments.

Shl1, Shl2

<shell | surface | prim | feature> The objects to be combined. All volume primitives and mechanical features will generate a geometric description as a shell, and thus can be used in this operation. Surfaces are internally converted to shells. Shells can also be constructed explicitly if desired.

Operation

<string> One of the set "+", "-", "*", or "/". These are interpreted as union, subtraction, intersection, and "cut," respectively. The cut operation uses the second object to cut a hole out of the first one, but no surfaces from the second object are included in the result (like a cookie cutter).

TriApxFlag(false)

<boolean> Optional flag. If true surface intersections are based on polygonal (triangular) approximations to the surfaces. This method works better on some models based on mechanical features.

Res(0.025)

<number> Optional. If TriApxFlag is true, then Res is used as the resolution to be used in computing the surface approximations. Smaller numbers produce better approximations.

combinerCrvs( Shl1, Shl2, Operation, TriApxFlag, Res )

Returns

<group> A group of intersection curves generated by performing the requested operation on Shl1 and Shl2.

Shl1, Shl2

<shell | surface | prim | feature> The objects to be combined. All volume primitives and mechanical features will generate a geometric description as a shell, and thus can be used in this operation. Surfaces are internally converted to shells. Shells can also be constructed explicitly if desired.

Operation

<string> One of the set "+", "-", "*", or "/". These are interpreted as union, subtraction, intersection, and "cut," respectively.

TriApxFlag(false)

<boolean> Optional flag. If true surface intersections are based on polygonal (triangular) approximations to the surfaces. This method works better on some models based on mechanical features.

Res(0.025)

<number> Optional. If TriApxFlag is true, then Res is used as the resolution to be used in computing the surface approximations. Smaller numbers produce better approximations.

Generally, the optional arguments are left off unless there are problems.

Basic Boolean Operations

Here is a simple example illustrating the three operations. First we start out with a box and a cylinder:

Box : boxFromAnchor( OriginAnchor, 1, 1, .5 );
Cir : circleCtrRad( pt( .5, .5 ), .35 );
Cyl : extrude( Cir, pt( 0, 0, .75 ), pt( 0, 0, -.25 ), true );

Note that true is used as the last argument to the extrude constructor so it returns a shell object (the data type that represents a solid). Here are the three basic operations, difference ("-"), intersection ("*"), and union ("+")

Solid : combineShells( Box, Cyl, "-" );

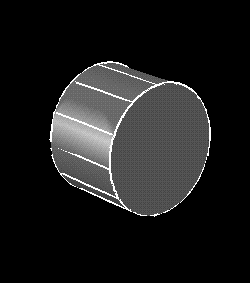
Solid : combineShells( Box, Cyl, "*" );

Solid : combineShells( Box, Cyl, "+" );

Multiple Operations

The result of combineShells is a shell and can be used in further operations. For example, we can subtract out another cylinder like this:

Cir2 : circleCtrRad( pt( .5, .5 ), .25 );
Cyl2 : extrude( Cir2, pt( 0, 0, .85 ), pt( 0, 0, -.35 ), true );

Solid2 : combineShells( Solid, Cyl2, "-" );

Cross Section Views

Another use for boolean operations is to produce cross-sectional views or cutaway views of complex parts. This should be done by constructing a surface for the cutting plane (i.e., don't use the plane object). Continuing with the above example, we construct a cutting surface and position it to cut Solid2 in half.

CuttingPlane : objTransform( flatSrf( 2, 2, 2, 2 ),
                             rx( -90 ), tx( .5 ), ty( .5 ) );

The first image shows Solid2 and CuttingPlane including the orientation of CuttingPlane (see more on orientation below).

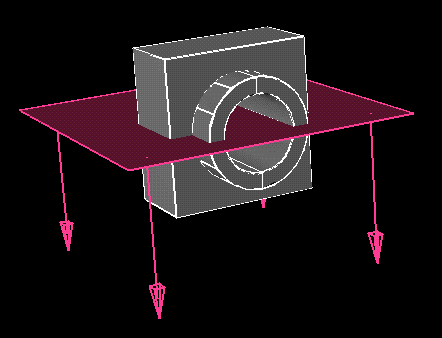
Now use the subtraction operation to create the cutaway view.

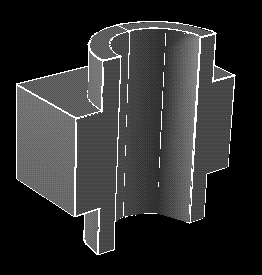
Cutaway : combineShells( Solid2, CuttingPlane, "-" );

Common Problems

The computation of solid models is based on the computation of the intersection of two surfaces and is a fairly fragile operation. There are a number of common problems and ways to avoid them.

Orientation

All the surfaces must be oriented such that the surface normals point into the solid. To determine if you have the corrent orientation use the Viewing Parameters dialog box in motif3d to view the surface normals.

Here's an example:

Cir : circleCtrRad( pt( .5, .5 ), .35 );
Cyl : extrude( Cir, pt( 0, 0, -.25 ), pt( 0, 0, .75 ), true );

Viewing the normals in motif3d show that the surfaces are inside out:

(Note that there are three surfaces in this example, the cylindrical one plus a disk on each end. There are four sample normal vectors displayed for each surface.)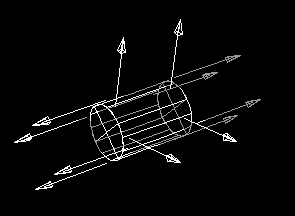

In this case, the orientation can be corrected in a number of ways. Here are three different ways to fix the orientation:

# Reverse the order of the points.
Cyl : extrude( Cir, pt( 0, 0, .75 ), pt( 0, 0, -.25 ), true );
# Reverse the circle.
Cyl : extrude( reverseObj( crvFromCircle( Cir )),
               pt( 0, 0, -.25 ),
               pt( 0, 0, .75 ), true );
# Reverse the whole thing.
Cyl : reverseObj( extrude( Cir,
                  pt( 0, 0, -.25 ), 
                  pt( 0, 0, .75 ), true ));

Now the normal vectors are correct. (The normals for the disk at each end are pointing at each other. The base points for these vectors are in the plane of each disk, but are located outside the disk itself due the trimmed surface construction that is used.)

See reverseObj for the full set of objects that can be reversed.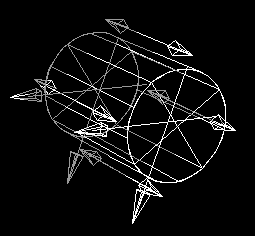

If the surfaces of a shell (solid) are inconsistantly oriented (i.e., some point in and some point out) this is a bug in the system and it should be reported. Use the Alpha_1 Bug Report form to submit a bug report.

Tangencies

Another source of problems is tangent (or near-tangent) surfaces, and coincedent surfaces. Here are some examples:

Cylinders with the same radii with intersecting axes.
Two solids with a single point of contact.
One surface that lies entirely in another surface (base of a cylinder which is coincident with a face of a box or the base of another cylinder for example).
Boundary curve of a surface that lies in another surface (same as above).
A boss on top of another boss (coincident surfaces).

Many of these problems can be worked around by creating models with small extensions. These extension are usually part of what is removed by the boolean operation so they do not affect the final result.

In the above example the second cylinder that is subtracted out to construct Solid2 is a little longer than the first cylinder (which it is effectively subtracted from).

Cyl : extrude( Cir, pt( 0, 0, .75 ), pt( 0, 0, -.25 ), true );
# Second cylinder needs a little extra.
Cyl2 : extrude( Cir2, pt( 0, 0, .85 ), pt( 0, 0, -.35 ), true );

Without the extension, the bases of the cylinders will be coincedent surfaces.

The geometric representations of the mechanincal features and process planning objects provide such extensions automatically so they will work with boolean operations.

Adjacencies

Sometimes it is necessary to create Adjacencies in order to make combineShells not crash. Adjacencies between surfaces "weld" or "sew" the surfaces together into boundary representations of volumetric objects. They are used primarily by combineShells to allow intersection curves with other objects to cross surface boundaries during the surface-trimming phase of the volume union, intersection, difference, and cut operations.

Adjacencies are automatically declared for the objects created by some operations, most notably the primitives and rounded primitives, and surface constructions which have a ShellFlag argument. This is at all times the preferred mechanism: adjacency declarations are tricky, and if the system will figure it out for you, you should take advantage of it.

In some cases, however, the adjacencies must be added manually after the surface construction operations. Adjacencies can only be declared between surfaces which are contained in the same shell. If both surfaces are not in the same shell, an error is signaled. Use mergeShell to merge them before attempting to declare the adjacency.

The simplest form of manual adjacency declares that an entire edge of one surface is adjacent (identical to) an entire edge of another surface. This might occur, for example, if the same curve was used in two different extrusion operations. The four natural boundary edges of a surface are identified by the names below:

"top" The low U edge, defined by the first row of the mesh.
"bottom" The high U edge, defined by the last row of the mesh.
"left" The low V edge, defined by the first column of the mesh.
"right" The high V edge, defined by the last column of the mesh.

Usually, the designer is not aware of which edge is which during the construction of the model. The simplest way at present to figure out this information is to use a construction like the following to cause the curve to be highlighted on the display. (This is a trial and error procedure, but better than nothing.)

TestCrv : getBoundary( Srf, "top" );
highlight( TestCrv );

#If surface is allready in a shell use
TestCrv : getBoundary( Shell[2], "top" );
highlight( TestCrv );

Note that the curve returned is simply one lying at the parametric boundary of the surface. If part of the surface is trimmed away, this will not be reflected in the returned curve.

Another method to check your shell for adjacencies is to call getUnsharedEdges. This function will return a list of all the edges in your shell that do not have an adjacency defined, along with the name of the boundary.

#Find all edges without adjacencies declared
edges : getUnsharedEdges(Shell)$;

If the adjacency which is being declared is not one in which the full boundaries are adjacent, then the parametric range of the overlapping section must be specified for each surface. A similar trial and error construction can be used for determining the correct parametric range:

TestCrv : regionFromCrv( getBoundary( Srf, "top" ), 0.0, 0.5 );
highlight( TestCrv );

There are three functions for declaring adjacencies by hand. Which one to use depends on the type of the adjacency being declared. For full boundary adjacencies, mkAdjacentFull is used. For partial boundary adjacencies, mkAdjacentPartial is used. In special cases, it may be necessary to use mkAdjacentTrim, which declares a full boundary of one surface adjacent to a full trimming curve in another surface. This will only be necessary for surfaces which are the result of the capSurface operation, and the most common operations (surfaces of revolution and extrusions) handle this type of declaration automatically.

# Right edge of surface 2 is adjacent to left edge 
# of surface 1.
mkAdjacentFull( BoxShell, 0, "left", 2, "right" );

# Surface has adjacent left and right edges.
mkAdjacentFull( CylinderShell, 0, "left", 0, "righ" );

mkAdjacentFull( Shell, Srf1, Side1, Srf2,Side2 )

Returns

<none> Adds adjacency attributes to both surfaces declaring the mutual adjacency. i.e. it modifies the surfaces in the shell; it does not create anything.

Shell

<shell> Shell containing surfaces to make adjacent.

Srf1, Srf2

<number> Indexes of the two surfaces which have an adjacent edge.

Side1, Side2

<string> One of the strings "top", "bottom", "left", or "right" indicating which edges are adjacent.

mkAdjacentPartial( Shell, Srf1, Edg1, P1S, P1E, Srf2, Edg2, P2S, P2E )

Returns

<none> Adds adjacency attributes to both surfaces declaring the mutual adjacency. i.e. it modifies the surfaces in the shell; it does not create anything

Shell

<shell> Shell containing surfaces to make adjacent.

Srf1, Srf2

<number> Indexes of the two surfaces which have an adjacent partial edge.

Edg1, Edg2

<string> One of the keywords "top", "bottom", "left", or "right" indicating which edges contain the adjacent portion.

P1S, P1E, P2S, P2E

<number> The parametric starting and ending values for the adjacent portion in the first and second surface respectively. Either pair of numbers may be given as a pair of False values to indicate that the full boundary is adjacent on that surface. If all four numbers are given as False, then the action of the routine is the same as the simpler call to mkAdjacentFull.

mkAdjacentTrim( Shell, TrimSrf, TrimEdge, BndSrf, BndEdge )

Returns

<none> Adds adjacency attributes to both surfaces declaring the mutual adjacency. i.e. it modifies the surfaces in the shell; it does not create anything

Shell

<shell> Shell containing surfaces to make adjacent.

TrimSrf

<number> The index of a trimmed surface in the shell. This is the surface containing the trimming curve which is part of the adjacency.

TrimEdge

<number> The index of a trimming loop in the trimmed surface which is to be the adjacent edge.

BndSrf

<number> The index of a surface in the shell containing the full boundary which is part of the adjacency.

BndEdge

<string> One of the keywords "top", "bottom", "left", or "right" indicating which boundary edge in this surface is adjacent to the trimming curve in the other surface.

C_Shape_Edit User's Manual Home Page

a1-web@gr.cs.utah.edu

`"top"`	The low U edge, defined by the first row of the mesh.
`"bottom"`	The high U edge, defined by the last row of the mesh.
`"left"`	The low V edge, defined by the first column of the mesh.
`"right"`	The high V edge, defined by the last column of the mesh.